SVM
In the real world we deal with data sets that are'nt linearly seperated.
As shown in the image below :
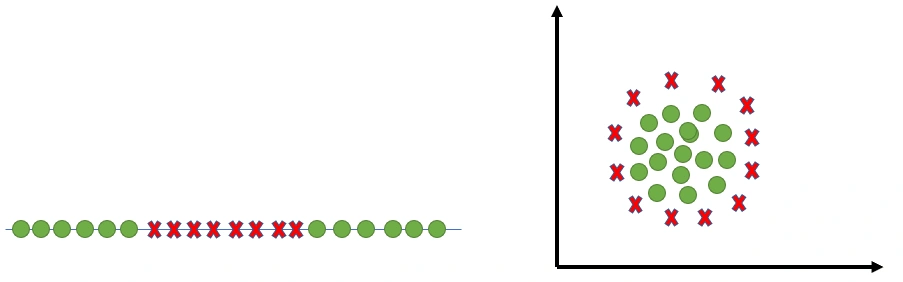
in our today's topic will discuss how SVM overcame this problem .
we will focus on :
1-why SVM
2-SVM parameters
Why SVM ?
Support Vectors are critical, as they contribute in the decision making of what class should a new data point belong to ( SVM is used in both classification and regression task)
our topic will go through the following phases :
maximum margin classifier => support vector classifier => support vector machine
1-Maximum margin :
maximum margin (hard margin) help us to create the decision boundary that best seperate the classes, but an overfitted model problem may arise .
2-Soft margin :
was use soft margin classifier to over come the overfitting model problem , allowing misclassification for the model .
therefore it can be generilized to new unseen data. we call it support vector classifier .
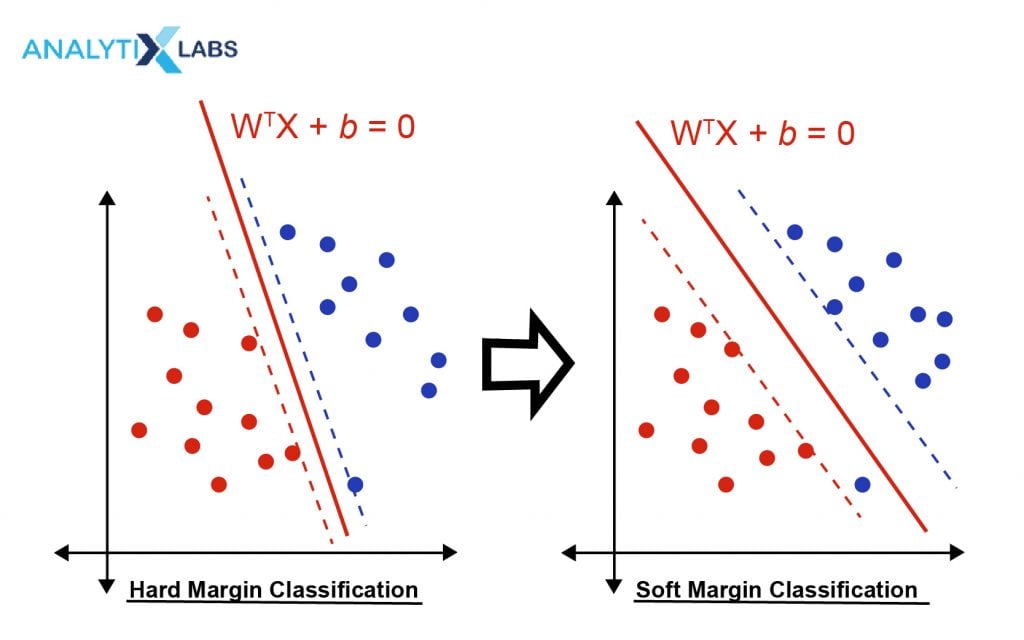
Notice both classifier operates in linearly seperated classes , but what if the data is'nt Linearly seperated ?
3-Support Vector Machine :
Handles data points that aren't linearly seperated , by projecting the data points to higher dimensions .
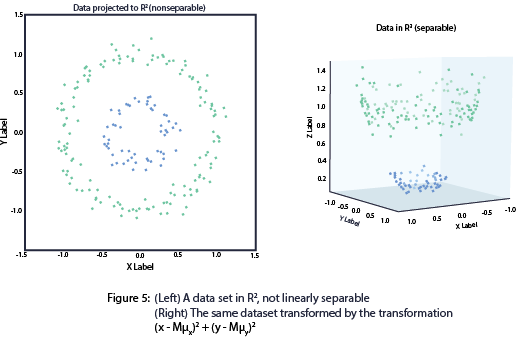
SVM Parameters :
First we need to know about margins.
margins in SVM:
1-soft margin manipulated by the C parameter
2-epsilon margin manipulated by the Epsilon parameter
C parameter :
1) adds soft margin ,data points that are spotted inside the margin or in the boundary of the margin are called support vectors .
2) Trade off between overfitted model with low error or a generilzed model with more errors
3) High C value : narrow margin => increase overfitting => less errors => less regularization
4) Low C value : larger margin => decrease overfitting => more errors => more regularization
Epsilon Parameter:
1) adds additional margin around the regression line allows tolerance of error
2) higher epsilon value means more tolerance for error and wider margin
3) errors in Epsilon margin aren't penalized unlike errors in soft margin
kernel parameter:
1) when the data is hard to seperate we need to project the data into higher dimensions
2) we can use poly, Radial Basis Function kernel,polynomial kerneles & the base case Linear Kernel.
Gamma Parameter:
1) it's essentially a parameter of the 'Radial Basis Kernel'& 'poly kernel' it determines how much influnce a single training instance has .
2) low gamma value means the influnce of each training instance is spread over a large area, reduce overfitting .
3) high gamma value means influnce of each training instance is confines over a small area, catching more noise.
